Translate this page into:
Exponential modelling of heart rate recovery after a maximal exercise
*Corresponding author: Elizabeth Tharion, Department of Physiology, Christian Medical College, Vellore, Tamil Nadu, India. e.tharion@cmcvellore.ac.in
-
Received: ,
Accepted: ,
How to cite this article: Joseph A, Kanthakumar P, Tharion E. Exponential modelling of heart rate recovery after a maximal exercise. Indian J Physiol Pharmacol 2023;67:125-30.
Abstract
Objectives:
Heart rate recovery (HRR) after exercise is clinically important as a predictor of mortality. In addition, HRR is an indicator of cardiac autonomic activity, since increased vagal activity and diminished sympathetic activity return the heart rate to resting conditions after exercise. The previous attempts to model HRR using polynomial, first-order and second-order modelling have produced mixed results. In this study, we hypothesised that the double-exponential fit would model the HRR more accurately than the single-exponential fit as it would capture the activity of both autonomic arms responsible for heart rate decay and investigated the outcome of these two models on the HRR data following a maximal exercise.
Materials and Methods:
Exponential curve fitting was done on a set of previously published data from our laboratory. The HRR data were acquired from 40 male participants (19–38 years) after a maximal treadmill exercise. The normalised HRR data from a 5-min time window from maximal heart rate were fitted using single and double-exponential curves, to obtain, respectively, the time constants Tau and, Tau 1 and Tau 2. The goodness-of-fit of the model was assessed with Chi-square values computed for each participant data set with both models. Considering that Chi-square of zero is a perfect fit, and therefore, smaller Chi-square values indicate a better fit than larger values, we computed the difference in the Chi-square values (Δχ2) between the models by subtracting the Chi-square value of the double-exponential fit from the Chi-square value of the single-exponential fit. This was based on the premise that if the calculated Δχ2 is positive, it would indicate a better fit with double-exponential than single-exponential decay model. The data are presented as mean ± standard deviation. Comparisons were made with Student’s t-test.
Results:
Data from four participants were excluded for technical reasons. The Tau of the single-exponential fit was 65.50 ± 12.13 s, while Tau 1 and Tau 2 of the double-exponential fit were 43.75 ± 18.96 s and 120.30 ± 91.32 s, respectively, the Tau 1 value being significantly lower than the Tau 2 value (P < 0.0001). Remarkably among the 36 participants, the difference in the Chi-square value was positive (127.2 ± 171.04) in 22 subjects and zero or marginally negative (−0.17 ± 0.31) in 14 subjects.
Conclusion:
Our results indicate that the double-exponential model fitted the HRR data better than the single-exponential model in almost two-thirds (61%) of our study population. In the remaining participants, the goodness-of-fit was nearly equivalent for both fits with no evidence of superior modelling with the single-exponential fit. Our data show that while the single-exponential fit is sufficient for modelling the HRR of 14 subjects, it was less efficient for fitting the data of most participants. In comparison, the double-exponential curve fit effectively modelled 100% of our study population. Given our findings, we conclude that the double-exponential model is more inclusive and better represented the HRR data of our study population than the single-exponential model.
Keywords
Heart rate recovery
Exponential curve fit
Time constant
Heart rate
Exercise
INTRODUCTION
The cardiac autonomic innervation is inaccessible for direct study. Many indirect parameters, including heart rate recovery (HRR) following exercise, are used to study it.[1] HRR is an independent predictor of all-cause mortality[2,3] and cardiovascular mortality[4,5] and is strongly related to physical fitness and maximal oxygen consumption.[6] Conventionally, HRR is considered an index of cardiac vagal reactivation,[7] though, on exercise termination, cardiac parasympathetic activity increases and cardiac sympathetic activity decreases, bringing the heart rate back to the resting level.
The post-exercise heart rate fall occurs in an exponential fashion reflecting the exponential kinetics of the underlying receptor action that produces parasympathetic reactivation and sympathetic withdrawal.[7] Multiple efforts have been undertaken to elucidate this decay using polynomial and first-order modelling,[4,8-11] but with limited success. Of these, some suggest that second-order models are the best fit for HRR following submaximal exercise,[8,10] while others recommend a double-exponential fit for the HRR curve.[7] Considering the latter to be more physiological as the heart rate decay is due to the synergistic action of two systems, both following first-order exponential relationships with different time constants and different profiles but ultimately leading to the decrease of a single component, namely, heart rate, from maximal to resting levels, we investigated the applicability of a double-exponential model on the HRR data obtained after maximal exercise. We hypothesised that the double-exponential model will be better than the single-exponential model in elucidating the physiological processes of sympathetic withdrawal and parasympathetic reactivation that underlies the return of the heart rate to the resting level after maximal exercise.
MATERIALS AND METHODS
The HRR data following a maximal treadmill exercise test, obtained from a group of Kungfu practitioners (n = 20) and their age, body mass index (BMI) and physical activity level-matched control group (n = 20), were taken for the analysis of exponential curve fitting reported here. Together, the groups comprised 40 male participants (19–38 years) who after written informed consent took part in the study. The original study that investigated physical fitness and cardiac autonomic control in these groups was published in 2020.[12]
HRR time constants
Real-time heart rate was acquired using the Polar wireless heart rate monitor belt (RS800Cx, Polar Electro, Finland) applied to the participant’s chest, which calculated heart rate based on 5-s samples of data. The heart rate was recorded throughout the maximal treadmill exercise protocol and for an additional 6 min during recovery after the exercise. The recovery heart rate was recorded while the participants were lying supine. A fixed ramp customised maximal protocol was programmed on the treadmill (RMS TMT MK II, Recorders and Medicare systems) for this study.
A 5-min time window of the heart rate from maximal heart rate and during the recovery period was analysed. The normalised HRR data were fitted using single and double-exponential curves.
The following formulae were used for the exponential curve fits:
(1) Single-exponential curve fit.
(2) Double-exponential curve fit.
x0 is an arbitrary minimum x-value determined by the fit algorithm; y0 is the estimated minimum y-value (or heart rate); A, A1 and A2 are coefficients of fit; and τ, τ1 and τ2 are decay constants (or time constants where x-axis represents time).
Single- and double-exponential fits were done using Igor Pro version 9 (WaveMetrics, USA). Representative single- and double-exponential fits of recovery heart rate from a subject are shown in [Figure 1]. The time constant obtained from the single-exponential fit is referred to as Tau, while the 2 time constants obtained from the double-exponential fit are referred to as Tau 1 and Tau 2. Chi-square values were computed for each data set with single- and double-exponential decay curves to estimate the goodness-of-fit of the model. Chi-square of zero is a perfect fit of the model to the data. The difference in the Chi-square values (Δχ2) of the 2 models was computed by subtracting the Chi-square value of the double-exponential fit from the Chi-square value of the single-exponential fit. If the difference in Chi-square values calculated in this manner is positive, it would indicate a better fit with double-exponential than single-exponential decay model. The smaller the Chi-square value the better the model fits the data.

- Representative single- and double-exponential fits of recovery heart rate from a subject. Tau: Time constant of single-exponential model, Tau 1 and Tau 2: Time constants of double-exponential model.
Further, to investigate whether the HRR data of either the Kungfu practitioners or the control subjects fitted better with the single or the double exponential curve fit, we compared the difference in Chi-square values (Δχ2) between the group of Kungfu practitioners (n = 18) and the control subjects (n = 18).
Statistical analysis
All data are presented as mean ± standard deviation (SD). Student’s t-test compared the time constants within the double-exponential fit, the time constants between the single- and double-exponential fits and the difference in Chi-square values (Δχ2) between the group of Kungfu practitioners and the control subjects. Microsoft Excel, Igor Pro (WaveMetrics, USA) and GraphPad Prism (version 5, San Diego, CA) were used for data analysis and representation. P < 0.05 was considered significant.
RESULTS
The heart rate data of four participants were not included in the analysis due to technical reasons, which included the inability to curve fit the heart rate data and because the time constants were outliers.
The time constants generated by the single-exponential fit and the double-exponential fit are given in [Table 1]. The mean ± SD value of Tau obtained with the single-exponential fit of the HRR data of 36 participants was 65.50 ± 12.13 s. The double-exponential fit of the same data gave a mean ± SD Tau 1 value of 43.75 ± 18.96 s and Tau 2 value of 120.30 ± 91.32 s. The Tau 1 value was significantly lower than the Tau 2 value (P < 0.0001). Further, Tau 1 was significantly lower than Tau (P < 0.0001) and Tau 2 was significantly higher than Tau (P < 0.001).
| Subject | Tau | Tau 1 | Tau 2 | Subject | Tau | Tau 1 | Tau 2 |
|---|---|---|---|---|---|---|---|
| 1 | 89.498 | 67.994 | 130.67 | 19 | 40.228 | 40.162 | 40.642 |
| 2 | 70.387 | 68.028 | 72.818 | 20 | 57.163 | 25.192 | 79.089 |
| 3 | 87.582 | 53.44 | 206.86 | 21 | 54.302 | 26.55 | 54.335 |
| 4 | 62.382 | 57.893 | 70.088 | 22 | 102.24 | 62.724 | 65.454 |
| 5 | 58.019 | 57.628 | 58.407 | 23 | 67.714 | 24.747 | 82.416 |
| 6 | 64.309 | 63.106 | 65.839 | 24 | 72.901 | 33.975 | 146.38 |
| 7 | 55.813 | 60.881 | 448.91 | 25 | 53.171 | 53.481 | 49.53 |
| 8 | 54.988 | 55.962 | 58.135 | 26 | 62.238 | 58.082 | 65.917 |
| 9 | 74.995 | 12.528 | 100.6 | 27 | 66.706 | 74.328 | 271.54 |
| 10 | 74.994 | 10.089 | 121.83 | 28 | 58.147 | 26.658 | 103.65 |
| 11 | 71.509 | 39.151 | 374.46 | 29 | 61.853 | 61.189 | 62.508 |
| 12 | 51.568 | 42.25 | 90.898 | 30 | 50.135 | 49.766 | 50.768 |
| 13 | 50.599 | 36.957 | 70.604 | 31 | 73.375 | 49.938 | 150.83 |
| 14 | 69.984 | 13.394 | 132.13 | 32 | 60.899 | 61.276 | 60.459 |
| 15 | 66.134 | 53.013 | 242.26 | 33 | 68.378 | 42.021 | 231.17 |
| 16 | 64.31 | 32.217 | 104.55 | 34 | 49.781 | 47.702 | 51.194 |
| 17 | 70.723 | 9.8654 | 95.613 | 35 | 72.773 | 70.44 | 74.784 |
| 18 | 72.959 | 10.427 | 75.174 | 36 | 75.386 | 21.939 | 170.46 |
Subjects 1–18 belong to Kungfu group. Subjects 19–36 belong to control group. n: Number of participants, HRR: Heart rate recovery, Tau: Time constant of single-exponential fit, Tau 1 and Tau 2: Time constants of double-exponential fit
Among the 36 participants, the difference in the Chi-square value was positive (127.2 ± 171.04) in 22 subjects and negative or zero (-0.17 ± 0.31) in 14 subjects [Figure 2]. The difference in the Chi-square values (Δχ2) of the Kungfu practitioners (112.76 ± 184.62) was not significantly different from those of the control group (42.56 ± 87.23) (P = 0.1539) [Figure 3].

- Plot of difference in Chi-square values (Δχ2) computed by subtracting the Chi-square value of the double-exponential fit from the Chi-square value of the single-exponential fit. Note that in 22 subjects (61%) the difference in Chi-square value is distinctly positive, indicating a better fit with double-exponential model in them. In 14 subjects, the difference is zero or minimally negative.
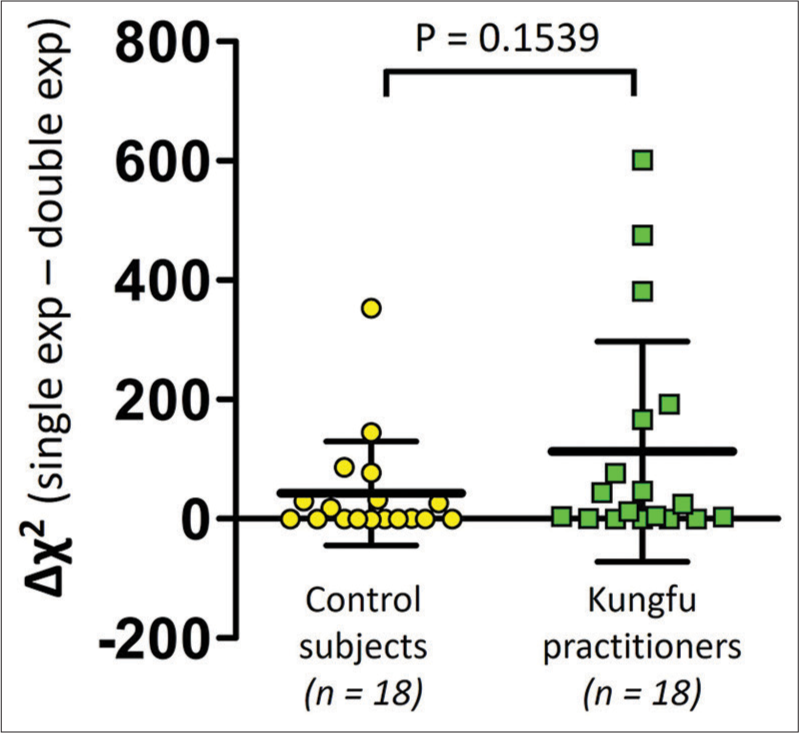
- Comparison of difference in Chi-square values (Δχ2) between Kungfu practitioners (green squares) and control subjects (yellow circles). n = Number of participants.
DISCUSSION
Our data reveal that the goodness of fit is better with the double-exponential decay model than with the single-exponential decay model in nearly two-thirds (61%) of the participants of our study. In the majority of these 22 participants, the Chi-square value of the single-exponential fit was greater than that of the double-exponential fit by a noteworthy magnitude [Figure 2]. The higher the Chi-square value, the lower the goodness of fit or the less the model fits the data. We observed that in 22 subjects, the Chi-square value of the single-exponential fit was greater than the double-exponential fit by a mean ± SD value of 127.2 ± 171.04. Of the remaining 14 subjects, the Chi-square value computed for both the models of fit was the same in one subject while in the remaining 13 participants, the Chi-square value of the double-exponential fit was marginally greater than the single-exponential fit [Figure 2]. In other words, the goodness of fit was equivalent for both models of fit in 14 subjects, the mean ± SD difference in Chi-square values between the fits being only −0.17 ± 0.31. The findings of our analysis indicate a clear superiority of the double-exponential fit over the single-exponential fit in 61% of our study participants, while there is no evidence to indicate that the single-exponential fit may be better in the remaining subjects.
As both wings of the autonomic nervous system act through receptors and hence act through first-order kinetics, various investigators have attempted to explain the heart rate decay after exercise through first-order kinetics.[4,7] However, these attempts have not borne fruit as the first-order exponential function is not a good model to explain recovery after a maximal exercise.[13] Pierpont and Voth have shown that despite this inability to fully model maximal exercise recovery satisfactorily, first-order kinetics can provide a reasonable model for submaximal exercise recovery[7] and Wang et al. have shown that the first-order time constant is a useful measure of fitness.[14]
An interesting speculation is whether a single system plays a major role in some individuals. Thus, parasympathetic reactivation may be the primary mode for decreasing heart rate from a maximum value in some people. In such conditions, first-order exponential modelling will give a good fit. If individuals have two processes working in tandem without one overpowering the other, then the double-exponential model could better explain the role of both processes. A maximal treadmill exercise protocol, as performed by the subjects of our study, would be expected to produce maximum sympathetic activation with release of catecholamines in the blood. The instant that such an exercise stops, inhibition of the cardiac vagal supply and stimulation of the cardiac sympathetic outflow by cortical and peripheral proprioceptive inputs would abruptly cease. However, cardiac sympathetic stimulation by the metaboreflex mechanism originating from the contracting muscles may continue for a further period slowing the HRR.[15,16] Moreover, the action of circulating catecholamines through their receptors on the sinoatrial node will also persist in a decremental manner.[17,18]
Thus, we conducted the current analysis on the heart rate data recorded during 5 min of recovery after a maximal treadmill exercise of 36 participants, hypothesising that since there are two exponents of the processes that underlie the recovery of heart rate from a maximum exercise, the double-exponential fit will be a more physiological technique to dissect the HRR. Modelling the recovery heart rate data with single and double-exponential decay curves produced different time constants or Tau values. This indicates that the two models described the data differently. When considering which model fits the data better, we found that the goodness of fit was distinctly better for the double-exponential model in 61% of the participants, and almost similar in the remaining subjects, in whom the results did not indicate a clear supremacy of the single-exponential model. It may be argued that the single-exponential curve fit is enough to model the HRR data in 14 of the subjects, probably because only a single component of the autonomic nervous system is predominantly responsible for the heart rate decay in them. Hence, the double-exponential curve fit did not give better results in these 14 subjects. However, applying only the single-exponential curve fit to all 36 subjects would have poorly modelled the data in 61% of our participants. On the other hand, had we applied only the double-exponential curve to all 36 subjects, we would still have satisfactorily modelled the HRR of 100% of our study participants. Thus, our data inform that the double-exponential curve fit is more inclusive than the single-exponential curve fit to model recovery heart rate after a maximal exercise.
The exploratory subgroup analysis that compared the difference in Chi-square values (Δχ2) between the group of Kungfu practitioners (n = 18) and the control subjects (n = 18) revealed no statistically significant difference between them [Figure 3]. This suggests that no one curve fitting (single exponential or double exponential) better modelled the HRR data of either the Kungfu practitioners or the control subjects. The control subjects were age, BMI and physical activity level matched to the Kungfu practitioners. From the distribution in [Figure 3], we perceive that the Δχ2 values are around the zero value in some participants of both groups, the values being definitely more positive in the remaining subjects in both groups, with more numbers with greater positivity in the Kungfu group. If the single-exponential curve fit alone had been applied, then the HRR data of all the participants in both groups would not have been modelled with adequate goodness of fit. Modelling with the double-exponential fit alone, on the other hand, would have acceptably captured the characteristics of HRR in all participants of both groups.
Of note, the absolute Chi-square values tend to be bigger when curve fits are done on large number of points due to larger statistical degrees of freedom. Therefore, it is essential to match the number of data points used while making the comparison between Chi-square values. Our study used 60 data points for all curve fits.
HRR kinetics continue to contribute to the field of autonomic dysfunction,[19] studies on ageing,[20] physical fitness[21] and sports science.[22,23] It is thus important to fully elucidate the nature of HRR dynamics as it is used in various scenarios of health and disease. Our findings contribute to the mathematical understanding of the physiological processes that underlie HRR and will stimulate further studies in the field as the quest for deeper knowledge in the field continues.
CONCLUSION
Our data reveal that the double-exponential curve unequivocally better modelled the post maximal exercise 5-min HRR data, than the single-exponential curve in majority (61%) of the participants of our study population. In the rest of the subjects, both fit modelled the recovery heart rates almost equally with no evidence to support an explicit edge for the single-exponential fit. Given these findings and the physiological fact that return of the heart rate to the resting level after a maximal exercise would necessarily involve both the processes of parasympathetic reactivation and waning of sympathetic action, we are inclined to conclude that the double-exponential fit is more suitable to model recovery heart rate after maximal exercise. Application of only the single-exponential curve fit may not accurately represent the HRR data of all subjects after a maximal exercise. Our data contribute to the knowledge base of kinetics of HRR after maximal treadmill exercise.
Declaration of patient consent
The Institutional Review Board (IRB) permission obtained for the study.
Conflicts of interest
There are no conflicts of interest.
Financial support and sponsorship
Nil.
References
- Pathophysiology of exercise heart rate recovery: A comprehensive analysis. Ann Noninvasive Electrocardiol. 2013;18:107-17.
- [CrossRef] [PubMed] [Google Scholar]
- Heart-rate recovery immediately after exercise as a predictor of mortality. N Engl J Med. 1999;341:1351-7.
- [CrossRef] [PubMed] [Google Scholar]
- Cardiopulmonary fitness and heart rate recovery as predictors of mortality in a referral population. J Am Heart Assoc. 2014;3:e000559.
- [CrossRef] [PubMed] [Google Scholar]
- Post-exercise heart rate recovery: An index of cardiovascular fitness. J Exerc Physiol Online. 2009;12:10-22.
- [Google Scholar]
- Heart rate recovery: Validation and methodologic issues. J Am Coll Cardiol. 2001;38:1980-7.
- [CrossRef] [PubMed] [Google Scholar]
- A study of maximum oxygen uptake and heart rate during work and recovery as measured on cycle ergometer on national Indian sportsmen. Br J Sports Med. 1979;13:24-8.
- [CrossRef] [PubMed] [Google Scholar]
- Assessing autonomic function by analysis of heart rate recovery from exercise in healthy subjects. Am J Cardiol. 2004;94:64-8.
- [CrossRef] [PubMed] [Google Scholar]
- Transient dynamics of ventilation and heart rate with step changes in work load from different load levels. Acta Physiol Scand. 1971;81:54-74.
- [CrossRef] [PubMed] [Google Scholar]
- Autonomic contribution to heart rate recovery from exercise in humans. J Appl Physiol Respir Environ Exerc Physiol. 1982;53:1572-5.
- [CrossRef] [PubMed] [Google Scholar]
- The effect of beta-adrenergic blockade on heart rate recovery from exercise. J Cardiopulm Rehabil Prev. 1989;9:202.
- [CrossRef] [Google Scholar]
- Vagally mediated heart rate recovery after exercise is accelerated in athletes but blunted in patients with chronic heart failure. J Am Coll Cardiol. 1994;24:1529-35.
- [CrossRef] [PubMed] [Google Scholar]
- Cardiac autonomic activity, physical fitness, and arterial blood pressure of Kungfu practitioners. Transl Sports Med. 2020;3:447-53.
- [CrossRef] [Google Scholar]
- Heart rate recovery post-exercise as an index of parasympathetic activity. J Auton Nerv Syst. 2000;80:169-74.
- [CrossRef] [PubMed] [Google Scholar]
- Time constant of heart rate recovery after low level exercise as a useful measure of cardiovascular fitness. Conf Proc IEEE Eng Med Biol Soc. 2006;2006:1799-802.
- [CrossRef] [PubMed] [Google Scholar]
- Heart rate recovery: Autonomic determinants, methods of assessment and association with mortality and cardiovascular diseases. Clin Physiol Funct Imaging. 2014;34:327-39.
- [CrossRef] [PubMed] [Google Scholar]
- Metaboreflex activation delays heart rate recovery after aerobic exercise in never-treated hypertensive men. J Physiol. 2016;594:6211-23.
- [CrossRef] [PubMed] [Google Scholar]
- Disappearance of norepinephrine from the circulation following strenuous exercise. J Appl Physiol Respir Environ Exerc Physiol. 1979;47:1311-4.
- [CrossRef] [PubMed] [Google Scholar]
- Plasma norepinephrine and heart rate dynamics during recovery from submaximal exercise in man. Eur J Appl Physiol Occup Physiol. 1989;58:879-83.
- [CrossRef] [PubMed] [Google Scholar]
- Relationship between heart rate recovery index and erectile dysfunction. North Clin Istanb. 2021;8:371-6.
- [CrossRef] [PubMed] [Google Scholar]
- Associations between heart rate recovery dynamics with estradiol levels in 20 to 60 year-old sedentary women. Front Physiol. 2018;9:533.
- [CrossRef] [PubMed] [Google Scholar]
- Estimation of heart rate recovery after stairclimbing using awrist-worn device. Sensors (Basel). 2019;19:2113.
- [CrossRef] [PubMed] [Google Scholar]
- Can a first-order exponential decay model fit heart rate recovery after resistance exercise? Clin Physiol Funct Imaging. 2015;35:98-103.
- [CrossRef] [PubMed] [Google Scholar]
- A single session of whole-body cryotherapy boosts maximal cycling performance and enhances vagal drive at rest. Exp Brain Res. 2023;241:383-93.
- [CrossRef] [PubMed] [Google Scholar]







